La lettre de la Preuve

ISSN 1292-8763

 
Atajos en las demostraciones

Ejemplos...

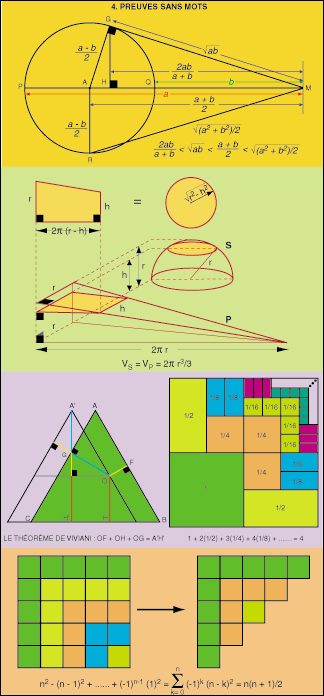
4. Pruebas sin palabras

 

5. Preuve heuristique impossible (aujourd'hui) à transformer en preuve formelle

On considère la suite des nombres entiers définie par :

x1 = 2,

x2 = [le plus petit facteur premier de x₁ + 1] =3,

x3 = [le plus petit facteur premier de x₁x₂ + 1] =7, ...,

xn+1 = [le plus petit facteur premier de x₁x₂... x_n + 1], ...

Le début est 2, 3 , 7, 43, 13, 53, 5, 6221671, 38709183810571, 139, 2801, 11, 17, 5471, ...

Cette suite d'Euclide-Mullin n'énumère que des nombres premiers différents. En effet, y_n = x₁x₂... x_n + 1 n'est pas divisible par x₁ (sinon 1 le serait comme différence de deux nombres divisibles par x₁). Le nombre yn n'est pas divisible par x₂ (sinon 1 le serait), etc. Puisque yn n'est divisible par aucun des nombres premiers, x₁, ...., x_n, x_n+1 est un nouveau nombre premier, et donc tous les x_i sont des nombres premiers distincts. La question est de savoir si cette suite énumère tous les nombres premiers sans en oublier (bien sûr, ce sera dans le désordre). On pense que oui et l'on propose la preuve heuristique suivante.

Supposons que la suite ne contienne pas tous les nombres premiers. Soit p le plus petit nombre premier qui n'est pas dans la suite. À partir d'un certain N, tous les nombres premiers inférieurs à p seront parmi les nombres
x₁, ..., x_N. Si n est un entier quelconque plus grand que N, le nombre yn = x₁x₂... x_{n + 1} peut être considéré comme un nombre quelconque vis-à-vis de p, et donc ce nombre a une chance sur p d'être un multiple de p (car un entier sur p est multiple de p). Le nombre yn a donc une probabilité de (1-1/p) de n'être pas multiple de p, qui est aussi la probabilité que x_n+1 soit différent de p. La probabilité pour que ni x_{N + 1} ni x_N+2... x_N+k ne soient égaux à p est donc (1&endash;1/p)^k qui tend vers 0 à l'infini. Autrement dit, la probabilité pour que p n'apparaisse pas dans la suite xn est nulle. Donc p apparaît dans la suite, ce qui contredit sa définition. Donc, tout nombre premier p apparaît dans la suite x_n, qui n'est pas autre chose que la liste des nombres premiers, sans répétition et écrite dans le désordre.
  Un tel raisonnement est presque bon, mais il suppose que y_n est tiré au hasard, ce qui n'est pas le cas, et donc, sans un complément (que personne n'a réussi à découvrir et qui semble hors de portée des méthodes mathématiques actuelles), la preuve heuristique n'est pas une preuve acceptable.

Regreso al texto