Preuve et perception III

Problème 1

Je prendrai le premier problème dans le livre de Papert "Jaillissement de l'esprit " (1980, Basic books, p. 146. Trad. française : 1981, Flammarion, p.182) :

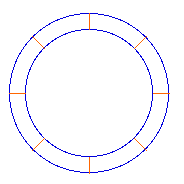"Imaginez donc une ficelle tendue autour de la circonférence de la Terre, que nous considérons ici comme un sphère absolument lisse, d'un rayon de six mille quatre cent quarante kilomètres. Quelqu'un propose de faire passer cette ficelle sur des poteaux de deux mètres de haut.
   Cette opération implique évidemment que la ficelle sera plus longue. Toute la question est de savoir de combien il faut l'allonger. La plupart de ceux qui ont fait des études secondaires savent comment trouver la réponse par un calcul.
   Mais avant d'effectuer ce calcul ou de poursuivre votre lecture, essayez donc de deviner : quelle longueur de ficelle faudra-t-il en plus ? Environ seize cents kilomètres ? ou cent soixante ? ou seize ?"

Papert alors, suggère de considérer une version analogue mais plus simple de ce problème :

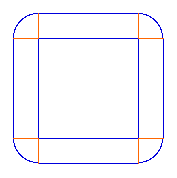"Une excellente règle générale, pour simplifier les choses, est d'en chercher une version linéaire. Nous posons donc le problème, mais pour une 'Terre carrée'."

 Augmenter la taille du carré ne change pas les secteurs en quart de cercle, et donc le supplément de ficelle nécessaire pour élever la ficelle au-dessus du sol à la hauteur h est la  même pour une très petite "Terre carrée" comme pour une très grande. Le problème est ainsi résolu. La quantité de ficelle supplémentaire nécessaire est (2ph). Papert lui-même affirme que le but de la recherche de ce problème n'est pas de donner la bonne réponse, "mais bien plutôt de s'efforcer de discerner le conflit que doivent soulever les différentes approches possibles du problème" (ibid.).

Une version linéaire différente et, peut être, plus consistante pourrait être suggérée par Leibniz :

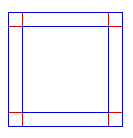
Mais Papert préfère continuer ainsi :

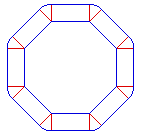
Quoiqu'il en soit, les deux façons d'opérer peuvent souligner le fait que les idées sous-jacentes montrent que la taille de la "terre" ne joue pas de rôle dans la détermination de la quantité de ficelle supplémentaire nécessaire. Cela résoud probablement le problème. Ainsi les deux idées, appelons-les Cur (idée de courbure) et Lin (idée de linéarité), apparaissent respectivement équivalentes pour le problème en question.

Manipuler le point vert

Mais ces deux idées apportent plus encore. Commençons par la version de Leibniz et, pour tout polygone régulier (carré, octogone, ...), appelons rayon la plus petite distance de son centre à son bord. Augmenter le rayon d'un polygone régulier de h accroit son périmètre du périmètre d'un polygone semblable de rayon h. Ceci est exactement la linéarité de la fonction représentée par la forme géométrique elle-même. Le tout est la somme de ses parties : si le rayon croit de x à (x+h), le périmètre croit de f(x) à f(x )+f(h).    Ainsi nous avons f(x+h )=f(x)+f(h) et f(0)=0. Le périmètre du polygone est une fonction linéaire de son rayon.Et le principe de continuité conduit au même résultat pour le cercle (il faut se souvenir que Leibniz fut le premier à employer systématiquement ce principe). La chose importante est que l'on peut lire directement ce fait sur les figures géométriques. Vous pouvez constater de vos propres yeux que l'agrandissement du périmètre est représenté par un polygone de même forme.

Pour suggérer une autre représentation, plus constructive, d'une fonction linéaire, Leibniz soulignerait le fait que la forme du polygone n'est pas changée en mettant la ficelle sur des potaux disposés autour sur son bord (c'est-à-dire en augmentant le rayon de h).

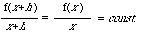et y = f(x) = c.x

Ces deux façons donnent une illustration de l'idée de conceptualisations fondées sur des formes (formbased).

Les potentialités de l'idée Cur de Papert peuvent être seulement appréciée dès lors que l'on considère l'expression algébrique y=c.x comme une forme nouvelle et pertinente. Il en va autrement du cas Leibniz où l'on obtient une seule et même fonction y=2p.x pour tous les types de 'Terre' (en fait le périmètre peut être toute courbe fermée continue ne se recoupant pas). Le facteur de proportionalité 1.(2p) indique le nombre des cercles complets que les poteaux sous-tendent en suivant la courbe. Ainsi les valeurs possibles de c seraient (n.(2p) n étant un entier quelconque) et du caractère discret de la portée on comprend immédiatement que de petites déformations de la courbe ne peuvent pas changer la valeur de c. L'objet géométrique en question n'est plus une courbe mais un champ de vecteurs le long d'une courbe. L'entier n est en général appelé indice de ce champ de vecteur relativement à la courbe. L'indice ne changera pas pour autant que les déformations de la courbe ne passent pas par un zéro du champ de vecteur.
   On pourrait déduire de tout cela une explication facile à comprendre justifiant le Théorème du point fixe de Brouwer.

Les deux approches résolvent le problème 1 et de ce point de vue apparaissent équivalentes. Nous allons maintenant présenter un second problème pour lequel les idées de Cur et Lin manifesteront qu'elles ne sont pas équivalentes. Nous prenons ce problème (un problème à propos de l'épicycloïde) dans le livre de Robert Davis "Learning mathematics " (Croom Helm, London 1984, 216pp.).

Problème 2

"Dans un test récent de ETS, une question porte sur un petit cercle qui roule, sans glisser, sur la circonférence d'un cercle plus grand (si l'on veut on pourrait voir là un engrenage). Le rayon du cercle le plus grand est trois fois celui du plus petit [...] Combien de fois voit-on le petit cercle réaliser une révolution complète ?"

Bob Davis continue:

"Il semble que les experts raisonnent essentiellement de la façon suivante : si le rayon du grand cercle est trois fois celui du petit alors son périmètre est trois fois plus grand. 'Rouler sans glisser' signifie que les longueurs d'arc sont égales. Comme la longueur d'un arc s est le produit du rayon par l'angle au centre, l'angle pour le petit cercle doit être trois fois celui pour le cercle plus grand. Mais l'angle pour le grand cercle doit croitre de 2p ; ainsi l'angle pour le petit cercle doit augmenter de 3.2p=6p, et donc le cercle accomplit trois révolutions (ou 'tours', ou 'rotations'). Cette réponse est fausse."

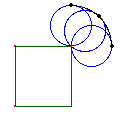Manifestement les experts essaient d'utiliser l'idée Lin. Considérons alors ce qui résulterait de l'utilisation de l'idée Cur. On remplace donc le grand cercle par un quadrilatère. On voit immédiatement (figure ci-contre) qu'aux quatre coins le petit cercle tourne sans avancer le long du périmètre de la plus grand figure. En remplaçant le grand cercle par ce quadrilatère nous sommes devenus capables de percevoir la superposition de deux mouvements distincts du petit cercle. Pour ainsi dire, le quadrilatère sépare ces deux mouvements du petit cercle. Comme il tourne de 90 degrés à chacun des quatre coins, on comprend immédiatement que la réponse correcte doit être quatre fois !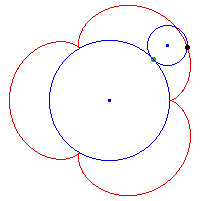
   Un point du petit cercle décrit une épicycloïde qui a trois "feuilles". C'est ce que l'idée Lin nous apprend. Bob Davis suggère aussi que les experts doivent avoir utilisé cette idée en la mettant mal en oeuvre parce qu'ils ont négligé la courbure ou plutôt les deux rotations différentes du petit cercle.

Pour être complet, je présente la solution proposée par Davis :

Dans la figure [figure suivante], C est le centre du petit cercle placé dans sa position de départ. Quelques instants après que le mouvement ait été engagé, le centre s'est déplacé en C'. Parce que le mouvement est réalisé sans glisser, l'arc BA' sur le petit cercle a la même longueur que l'arc AB sur le grand cercle. Donc l'angle BC'A' est trois fois l'angle AOB. Mais dès que nous disposons d'une droite de référence qui ne tourne pas, PC', qui se translate pour toujours passer par le centre du petit cercle, nous voyons aisément que l'angle BC'A' n'est pas l'angle dont le petit cercle a tourné.

C'est en revanche le cas de l'angle PC'A'. Le reste de la solution relève maintenant de la routine [...] Le petit cercle réalise exactement quatre révolutions -- ou "tours", ou "rotations" [...] Notons que la représentation fausse est très proche d'être correcte. Si une roue de bicyclette qui a un périmètre de 87 pouces tourne sans clisser sur un trottoir plat, et couvre une distance de 3.87=261 pouces, alors la roue aura effectué exactement trois rotations. On peut penser que des représentations cognitives de ce phénomène ont refait surface, ou ont été construites, par les experts pour qu'ils se soient tous mis d'accord... sur la réponse fausse [parce qu'ils ont utilisé seulement l'idée Lin].

Comme dans le cas de l'analyse de Papert pour le problème 1, cette présentation du problème 2 est très fortement influencée par la préoccupation traditionnelle pour les formules. La voie Leibnizienne, en revanche, est plus attentive au relation structurelles et aux objets intuitifs.

(Retour à la première page)

---

Cabri Java Project