Raccourcis dans les
démonstrations
par
Jean-Paul Delahaye
Universite des Sciences et Technologies de Lille
Des
exemples...

1. Indigestes
systèmes formels

La codification des démonstrations rend celles-ci
testables par ordinateur, mais pas très
agréables aux humains. L'un des premiers
systèmes entièrement codifiés de
preuves est celui de B. Russell et A. Whitehead, qui ont
essayé de rester le plus près possible du
formalisme qu'ils définissaient. Voici un extrait de
leur ouvrage Principia Mathematica, proposé ici pour
en montrer l'intérêt... esthétique. On
reconnaît en 52.21 un énoncé qui
signifie que l'ensemble vide (le V retourné) n'est
pas élément de 1 qui, par définition,
dans ce système, est la classe de toutes les classes
ayant un seul élément. Chaque
énoncé est soigneusement justifié par
sa preuve donnée juste après, qui en permet,
en théorie, la vérification mécanique.
Pas un mot n'apparaît.

2. Les abus dans les
exposés mathématiques
Les raccourcis et omissions pratiqués lors
d'exposés sont bien pires que ceux qu'on trouve dans
les textes écrits. Des recensions humoristiques de
ces abus ont plusieurs fois été
proposées. En voici une, largement inspirée
par celle de la revue Plot (APMEP Orléans-Tour,
n° 86).
o Démonstration par l'évidence :
"La démonstration est triviale" ; "Immédiat
à partir des définitions" ; "On obtient
sans peine que..." ; "On voit que..."
o Démonstration par la confiance : "Vous n'avez
qu'à essayer, vous verrez, ça marche".
Variante : "Je l'ai démontré hier chez moi,
aucune difficulté."
o Démonstration par consensus : "Tous ceux qui
sont d'accord lèvent la main". Variante encore
plus efficace : "Tous ceux qui ne sont pas d'accord
lèvent la main."
o Démonstration par commodité
dénommée "nos désirs sont des
réalités" : "Ce serait si beau si
c'était vrai, donc..." (Redoutablement
dangereuse.)
o Démonstration par nécessité :
"Ça doit être vrai, sinon toutes les
mathématiques s'effondreraient." Variante : "Le
cas contraire contredirait un résultat bien connu
qui ne peut pas être faux." (Peu de travail est
nécessaire pour en tirer une bonne vieille preuve
par l'absurde.)
o Démonstration par plausibilité :
"Ça a l'air bon, donc ça doit être
vrai." (Très utilisé pour évaluer le
résultat d'un long calcul ; ne pas en abuser.)
o Démonstration par intimidation : "Ne soyez
pas stupide! Bien sûr que c'est vrai." Variantes du
débutant : "Même un débutant sait
ça" ; "Vous l'avez vu en sixième"."
Variante du devoir pour demain : "Ceux qui en doutent
feront la démonstration pour demain sur une
feuille qu'ils me rendront." Variante du tableau : "Si
quelqu'un a des doutes, il passe au tableau le
démontrer."
o Démonstration par manque de temps : "Il ne me
reste pas assez de temps, vous ferez la
démonstration vous-même."
o Démonstration par complexité : "La
démonstration est trop compliquée pour
être donnée ici." Variantes : "Je ne peux
pas vous le faire, car ça fait partie du programme
de l'année prochaine." "J'ai fait le calcul en
1985, c'est assez pénible, je n'ai pas envie de le
refaire."
o Démonstration par accident : "Tiens, tiens,
qu'avons-nous là..." (En fait, tout était
calculé par avance pour obtenir le résultat
prétendument inattendu.)
o Démonstration par la définition dite
méthode du postulat d'Euclide : "On le
définit comme vrai." (En abuser risque de diminuer
l'intérêt de votre cours.)
o Démonstration par la tautologie : "C'est
vrai, parce que c'est vrai." (Risque de vous faire perdre
du crédit, mieux vaut utiliser une des autres
méthodes.)
o Démonstration par référence :
"Comme c'est établi à la page 289 du ..."
(Là encore, si vous en abusez, vous viderez votre
cours de sa substance.)
o Démonstration par perte de
référence : "Je sais que j'ai vu la
démonstration quelque part." (Même si c'est
du bluff, préférez la méthode
précédente.)
o Démonstration par manque
d'intérêt : "Y a-t-il quelqu'un qui souhaite
vraiment voir la démonstration?" Variante en
combinant avec la démonstration par
complexité : "La démonstration est longue
et pénible. Est-ce que je la fais?" Variante dite
du calcul merdique : "En général, quand je
me lance dans ce calcul, je me plante. On y va?"
o Démonstration par obstination : "Vous pouvez
croire ce que vous voulez, moi je vous dis que c'est
vrai." Variante du contre-exemple : "Trouvez-moi un
contre-exemple, en attendant je considère que
c'est vrai." (Contraire à la déontologie la
charge de la preuve ne serait pas à celui qui
affirme.)
o Démonstration par analogie : "C'est la
même chose que..." ; "Il suffit de s'inspirer
de..." "On procède comme pour..." (Moyen efficace
d'obtenir des résultats faux : le
procédé a coûté cher à
de nombreux mathématiciens.)
o Démonstration par autorité :
"Borsnbuch l'a dit." Variante dite de l'ascenseur : "J'ai
rencontré Borsnbuch dans l'ascenseur, et il est
d'accord."
o Démonstration par symbolisme excessif : "a
> 0 $b > a
F(ÿA(a)) > 0
ŸB(b)fi ..." Variante
dite du renvoi multiple : "On conclut en combinant les
lemmes 1, 3, 8 et 15 avec le théorème 12,
puis en utilisant les propositions 7, 9 et 21."
o Démonstration par appel à l'opinion
publique : "Si c'était vrai ça se saurait,
donc c'est faux..." (Contrairement aux apparences, ce
procédé marche bien, car les
résultats simples qui n'ont pas été
démontrés sont généralement
faux.)

3. Le vide et les
entiers de Von Neumann
Un exemple remarquable de situation où un
formalisme élégant conduit à des
notations impraticables si on ne les accompagne pas de
notations raccourcies est celui des entiers de von Neumann,
qui permettent en théorie des ensembles de construire
les nombres à partir de l'ensemble vide. Ceux-ci sont
définis en posant 0 = {} (l'ensemble vide), n + 1 = n
" {n}, ce qui donne :
0 = {}
1 = {{}}
2 = {{}, {{}}}
3 = {{}, {{}}, {{}, {{}}}}
4 = {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}}
5 = {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}},
{{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}}}
6 = {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}},
{{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}}, {{},
{{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}, {{}, {{}}, {{},
{{}}}, {{}, {{}}, {{}, {{}}}}}}}
7 = {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}},
{{}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}}, {{},
{{}}, {{}, {{}}}, {{}, {{}}, {{}, {{}}}}, {{}, {{}}, {{},
{{}}}, {{}, {{}}, {{}, {{}}}}}}, {{}, {{}}, {{}, {{}}},
{{}, {{}}, {{}, {{}}}}, {{}, {{}}, {{}, {{}}}, {{}, {{}},
{{}, {{}}}}}, {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{},
{{}}}}, {{}, {{}}, {{}, {{}}}, {{}, {{}}, {{},
{{}}}}}}}}
Imagine-t-on combien il serait pénible
d'écrire les tables de multiplication dans ce
formalisme!

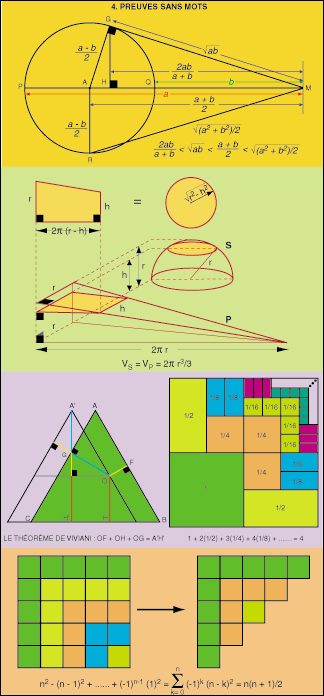
4. Preuves sans
mots

5. Preuve
heuristique imossible (aujourd'hui) à transformer en
preuve formelle
On considère la suite des nombres entiers
définie par :
x1 = 2,
x2 = [le plus petit facteur premier de
x1 + 1] =3,
x3 = [le plus petit facteur premier de
x1x2 + 1] =7, ...,
xn+1 = [le plus petit facteur premier de
x1x2... xn + 1],
...
Le début est 2, 3 , 7, 43, 13, 53, 5, 6221671,
38709183810571, 139, 2801, 11, 17, 5471, ...
Cette suite d'Euclide-Mullin n'énumère que
des nombres premiers différents. En effet,
yn = x1x2... xn
+ 1 n'est pas divisible par x1 (sinon 1 le serait
comme différence de deux nombres divisibles par
x1). Le nombre yn n'est pas divisible par
x2 (sinon 1 le serait), etc. Puisque yn n'est
divisible par aucun des nombres premiers, x1,
...., xn, xn+1 est un nouveau nombre
premier, et donc tous les xi sont des nombres
premiers distincts. La question est de savoir si cette suite
énumère tous les nombres premiers sans en
oublier (bien sûr, ce sera dans le désordre).
On pense que oui et l'on propose la preuve heuristique
suivante.
Supposons que la suite ne contienne pas tous les nombres
premiers. Soit p le plus petit nombre premier qui n'est pas
dans la suite. À partir d'un certain N, tous les
nombres premiers inférieurs à p seront parmi
les nombres
x1, ..., xN. Si n est un entier
quelconque plus grand que N, le nombre yn =
x1x2... xn + 1 peut
être considéré comme un nombre
quelconque vis-à-vis de p, et donc ce nombre a une
chance sur p d'être un multiple de p (car un entier
sur p est multiple de p). Le nombre yn a donc une
probabilité de (1-1/p) de n'être pas multiple
de p, qui est aussi la probabilité que
xn+1 soit différent de p. La
probabilité pour que ni xN + 1
ni xN+2... xN+k ne soient égaux
à p est donc (1&endash;1/p)k qui tend vers
0 à l'infini. Autrement dit, la probabilité
pour que p n'apparaisse pas dans la suite xn est nulle. Donc
p apparaît dans la suite, ce qui contredit sa
définition. Donc, tout nombre premier p
apparaît dans la suite xn, qui n'est pas
autre chose que la liste des nombres premiers, sans
répétition et écrite dans le
désordre.
Un tel raisonnement est presque bon, mais il
suppose que yn est tiré au hasard, ce qui
n'est pas le cas, et donc, sans un complément (que
personne n'a réussi à découvrir et qui
semble hors de portée des méthodes
mathématiques actuelles), la preuve heuristique n'est
pas une preuve acceptable.

|